Reading time 9 minutes

STAAR framework - variant-set test using annotation

26 Apr 2023 - last update

Abbreviations

  • COSI: Calibration Coalescent Model
  • FAVOR: Functional Annotations of Variants - Online Resource
  • GWAS: Genome-Wide Association Study
  • MAF: Minor Allele Frequency
  • RVAT: Rare-Variant Association Test
  • SKAT: Sequence Kernel Association Test
  • STAAR: variant-set test for association using annotation Information
  • STAAR-O: STAAR with multiple annotation weights (Omnibus Test)
  • SCANG-STAAR: SCANG (scan the genome) method combined with STAAR
  • WGS: Whole-Genome Sequencing
  • WES: Whole-Exome Sequencing

Overview

The SKAT (Sequence Kernel Association Test) method is fundamental to the STAAR (variant-Set Test for Association using Annotation information) framework. STAAR builds upon the SKAT method by incorporating multiple functional annotations for genetic variants to improve the power of the association tests. The integration of annotation information in STAAR allows prioritization of functional variants using multidimensional variant biological functions.

The authors target:

  1. Limitations of existing methods: Current approaches for RV analysis of WGS/WES studies have limited ability to define analysis units in the noncoding genome.
  2. Proposed framework: Introduce a computationally efficient and robust noncoding RV association detection framework for WGS data.
  3. Gene-centric analysis: Propose additional strategies for grouping noncoding variants based on functional annotations within STAAR.
  4. Non-gene-centric analysis: Propose SCANG-STAAR, a flexible data-adaptive window size RVAT method that incorporates multiple functional annotations and accounts for relatedness and population structure.
  5. STAARpipeline: Develop a pipeline that functionally annotates both noncoding and coding variants of a WGS study and performs RVATs using the proposed methods for both gene-centric and non-gene-centric analysis.

First, the rare-variant association tests (RVATs) are defined to analyse rare variants in association with phenotypes. Then, STAAR is applied, which incorporates multiple functional annotations for genetic variants to boost power in RVATs. STAAR can be applied in different ways, such as STAAR-O, which uses multiple annotation weights. Additionally, for non-gene-centric analysis, SCANG-STAAR is proposed, which uses dynamic windows with data-adaptive sizes and incorporates multidimensional functional annotations.

Method

  1. Notations and model:
    • Generalized linear model for unrelated samples (Equation 1):
      \(g(\mu_i) = \alpha_0 + \boldsymbol{X}_i^T\alpha + \boldsymbol{G}_i^T\beta\)
    • Generalized linear mixed model for related samples (Equation 2):
      \(g(\mu_i) = \alpha_0 + \boldsymbol{X}_i^T\alpha + \boldsymbol{G}_i^T\beta + b_i\)
  2. Variant-set test using STAAR:
    • Burden test statistic:
      \(Q_{\mathrm{Burden},l,k} = \left(\sum_{j=1}^p \hat{\pi}_{jk}w_{jl}S_j\right)^2\)
    • SKAT test statistic:
      \(Q_{\mathrm{SKAT},l,k} = \sum_{j=1}^p \hat{\pi}_{jk}w_{jl}^2S_j^2\)
    • ACAT-V test statistic:
      \(Q_{\mathrm{ACAT-V},l,k} = \overline{\hat{\pi}_{\cdot k}w_{\cdot l}^2\mathrm{MAF}(1 - \mathrm{MAF})}\tan\left((0.5 - p_{0,k})\pi\right) + \sum_{j=1}^{p'} \hat{\pi}_{jk}w_{jl}^2\mathrm{MAF}_j(1 - \mathrm{MAF}_j)\tan\left((0.5 - p_j)\pi\right)\)
  3. STAAR tests:
    • STAAR-Burden (STAAR-B):
      \(T_{\mathrm{STAAR-B}} = \sum_{l=1}^2\sum_{k=0}^K\frac{\tan\{(0.5 - p_{\mathrm{Burden},l,k})\pi\}}{2(K+1)}\)
    • STAAR-S:
      \(T_{\mathrm{STAAR-S}} = \sum_{l=1}^2\sum_{k=0}^K\frac{\tan\{(0.5 - p_{\mathrm{SKAT},l,k})\pi\}}{2(K+1)}\)
    • STAAR-ACAT-V (STAAR-A):
      \(T_{\mathrm{STAAR-A}} = \sum_{l=1}^2\sum_{k=0}^K\frac{\tan\{(0.5 - p_{\mathrm{ACAT-V},l,k})\pi\}}{2(K+1)}\)
    • STAAR-O test statistic:
      \(T_{\mathrm{STAAR-O}} = \frac{1}{3}\left[\tan\{(0.5 - p_{\mathrm{STAAR-B}})\pi\} + \tan\{(0.5 - p_{\mathrm{STAAR-S}})\pi\} + \tan\{(0.5 - p_{\mathrm{STAAR-A}})\pi\}\right]\)
  4. Dynamic window analysis using SCANG-STAAR:
    • Minimum P value of all candidate moving windows:
      \(p_{\mathrm{min}} = \min_{L_{\mathrm{min}} \le |I| \le L_{\mathrm{max}}}p(I)\)
  5. Conditional analysis
    • The STAARpipeline performs conditional analysis to identify RV association independent of known variants. We first select a list of known variants by including the trait-associated variants identified in literature, for example, variants indexed in the GWAS Catalog or significant variants in large-scale GWAS. The significant variants detected in individual analyses using the same data could also be added into the known variants list to ensure the RV signals are not captured by the significant individual variants. We then use the following stepwise selection strategy to select a subset of independent variants representing the known variant list as the variants adjusted in the conditional analysis:
      1. Calculate the individual P value of all variants in the known variants list and select the most significant variant.
      2. For each step, calculate the P values of all the remaining variants conditional on the variant(s) that have already been selected. For each variant, we only condition on the selected variants within a specified region of that variant, such as the \(\pm\)1-Mb window.
      3. Select the variant with minimum conditional P value that is lower than the cutoff P value, for example, \(1 \times 10^{-4}\).
      4. Repeat steps 2–3 until no variants can be selected. Finally, we calculate the conditional P value of each significant RV analysis unit by adjusting for the selected variants residing in an extended region (for example, \(\pm\)1-Mb window) of the analysis unit.

Type I error rate simulations

The authors perform this as follows:

  1. 100,000 sequencing chromosomes in a 10-Mb region
  2. African American population linkage disequilibrium structure (COSI)
  3. Total sample sizes (n = 50,000)
  4. Continuous traits from a linear model:
    \(Y_i = 0.5X_{1i} + 0.5X_{2i} + {\it{\epsilon }}_i\),
    \(X_{1i} \sim N(0,1)$, $X_{2i} \sim \mathrm{Bernoulli}(0.5)\), \(\epsilon_i \sim N(0,1)\)
  5. Dichotomous traits from a logistic model:
    \(\mathrm{logit}\,P(Y_i = 1) = \alpha_0 + 0.5X_{1i} + 0.5X_{2i}\),
    \(X_{1i}\) and \(X_{2i}\) defined as in continuous traits, \(\alpha_0\) for 1% prevalence
  6. Case–control sampling
  7. Ten annotations generated: \(A_1, \ldots, A_{10}\) as i.i.d. \(N(0,1)\) for each variant
  8. SCANG-STAAR-S, SCANG-STAAR-B, SCANG-STAAR-O with MAF and ten annotations as weights
  9. 10,000 replicates for genome-wise (family-wise) type I error rates at α = 0.05 and 0.01

Using ACAT in STAAR

The Aggregated Cauchy Association Test (ACAT) is a statistical method used for rare-variant association tests (RVATs) in genetic studies. ACAT is designed to aggregate the association signals of multiple rare genetic variants within a genomic region or a gene, while accounting for the directions of the effects of these variants on the phenotype of interest. The ACAT method utilizes a Cauchy distribution, which allows for improved performance in identifying true associations, especially when the directions and magnitudes of variant effects are heterogeneous.

In a separate page, I discuss the ACAT method. Some of the following passages are included in both pages since they related.

Figure 1. Slide from presentation of ACAT method by Dr. Xihong Lin.

Noncoding rare-variant association tests

The authors propose the following:

  1. Noncoding RVAT framework: Propose a computationally efficient and robust noncoding rare-variant association test (RVAT) framework for phenotype-genotype association analyses of WGS data.
  2. Regression-based: Allows adjustment for covariates, population structure, and relatedness by fitting linear and logistic mixed models for quantitative and dichotomous traits.
  3. Gene-centric approach: Group noncoding rare variants for each gene using eight functional categories of regulatory regions and apply STAAR, which incorporates multiple in silico variant functional annotation scores.
  4. Non-gene-centric approach: Propose SCANG-STAAR, using dynamic windows with data-adaptive sizes and incorporating multidimensional functional annotations instead of fixed-size sliding windows.
  5. Conditional analysis: Perform analytical follow-up to dissect RV association signals independent of known variants.

Applying STAAR-O for multiple annotation weights

In the STAAR Nature Methods paper, the section Gene-centric analysis of the noncoding genome shows how the STAAR method can indeed be used to capitalize on the ACAT method to obtain a combined p-value from a set of annotations for a single variant. The STAAR framework incorporates multiple functional annotation scores into the RVATs (rare-variant association tests) to increase the power of association analysis. In this context, it uses the STAAR-O test, an omnibus test that aggregates annotation-weighted burden test, SKAT, and ACAT-V within the STAAR framework.

By incorporating multiple functional annotation scores, such as CADD, LINSIGHT, FATHMM-XF, and annotation principal components (aPCs), the STAAR method enhances the ability to detect associations between variants and traits of interest. Therefore, the STAAR framework can be used to leverage the strengths of the ACAT method and obtain a combined p-value from a set of annotations for a single variant or a set of variants.

Non-gene-centric analysis using dynamic windows with SCANG-STAAR

The SCANG-STAAR method is an improvement over the fixed-size sliding window RVAT in the STAAR framework. It proposes a dynamic window-based approach called SCANG-STAAR, which extends the SCANG procedure by incorporating multidimensional functional annotations. This method allows for flexible detection of locations and sizes of signal windows across the genome, as the locations of regions associated with a disease or trait are often unknown in advance, and their sizes may vary across the genome. Using a prespecified fixed-size sliding window for RVAT can lead to power loss if the prespecified window sizes do not align with the true locations of the signals.

The SCANG-STAAR method has two main procedures: SCANG-STAAR-S and SCANG-STAAR-B. SCANG-STAAR-S extends the SCANG-SKAT (SCANG-S) procedure by calculating the STAAR-SKAT (STAAR-S) p-value in each overlapping window by incorporating multiple variant functional annotations, instead of using just the MAF-weight-based SKAT p-value. SCANG-STAAR-B is based on the STAAR-Burden p-value. SCANG-STAAR-S has two advantages over SCANG-STAAR-B in detecting noncoding associations using dynamic windows: first, the effects of causal variants in a neighborhood in the noncoding genome tend to be in different directions, especially in intergenic regions; second, due to the different correlation structures of the two test statistics for overlapping windows, the genome-wide significance threshold of SCANG-STAAR-B is lower than that of SCANG-STAAR-S.

SCANG-STAAR also provides the SCANG-STAAR-O procedure, based on an omnibus p-value of SCANG-STAAR-S and SCANG-STAAR-B calculated by the ACAT method. However, unlike STAAR-O, the ACAT-V test is not incorporated into the omnibus test because it is designed for sparse alternatives, and as a result, it tends to detect the region with the smallest size that contains the most significant variant in the dynamic window procedure.

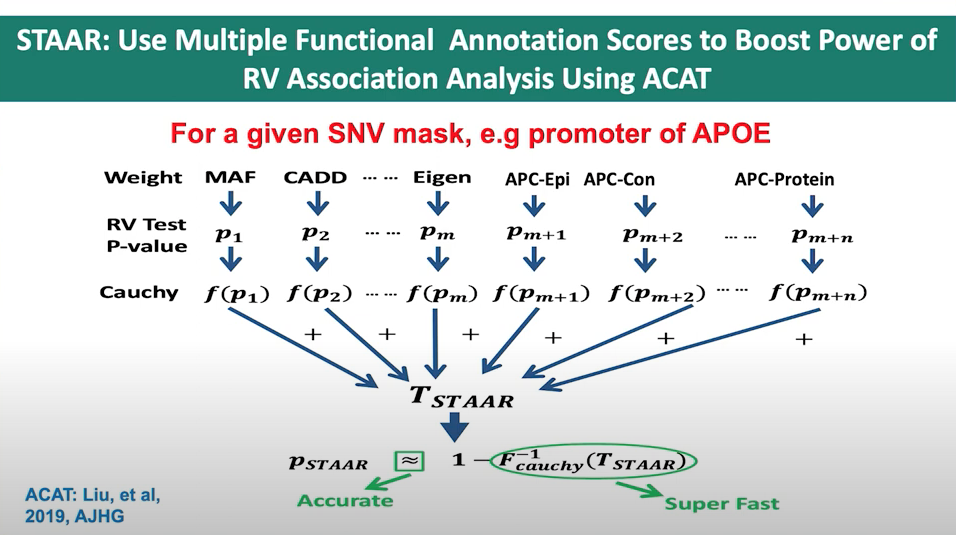
Figure 2. Slide from presentation of ACAT application in STAAR by Dr. Xihong Lin.

Multi-weight annotation analysis

The STAAR framework can be used to combine the p-values associated with each of the 5 annotation columns (CADD_score, MAF, GnomAD_AF, REVEL_score, ClinVar_score) for a single variant. STAAR incorporates multiple functional annotation scores as weights when constructing its statistics, making it suitable for combining p-values from different annotation columns to obtain a single combined p-value for that variant.

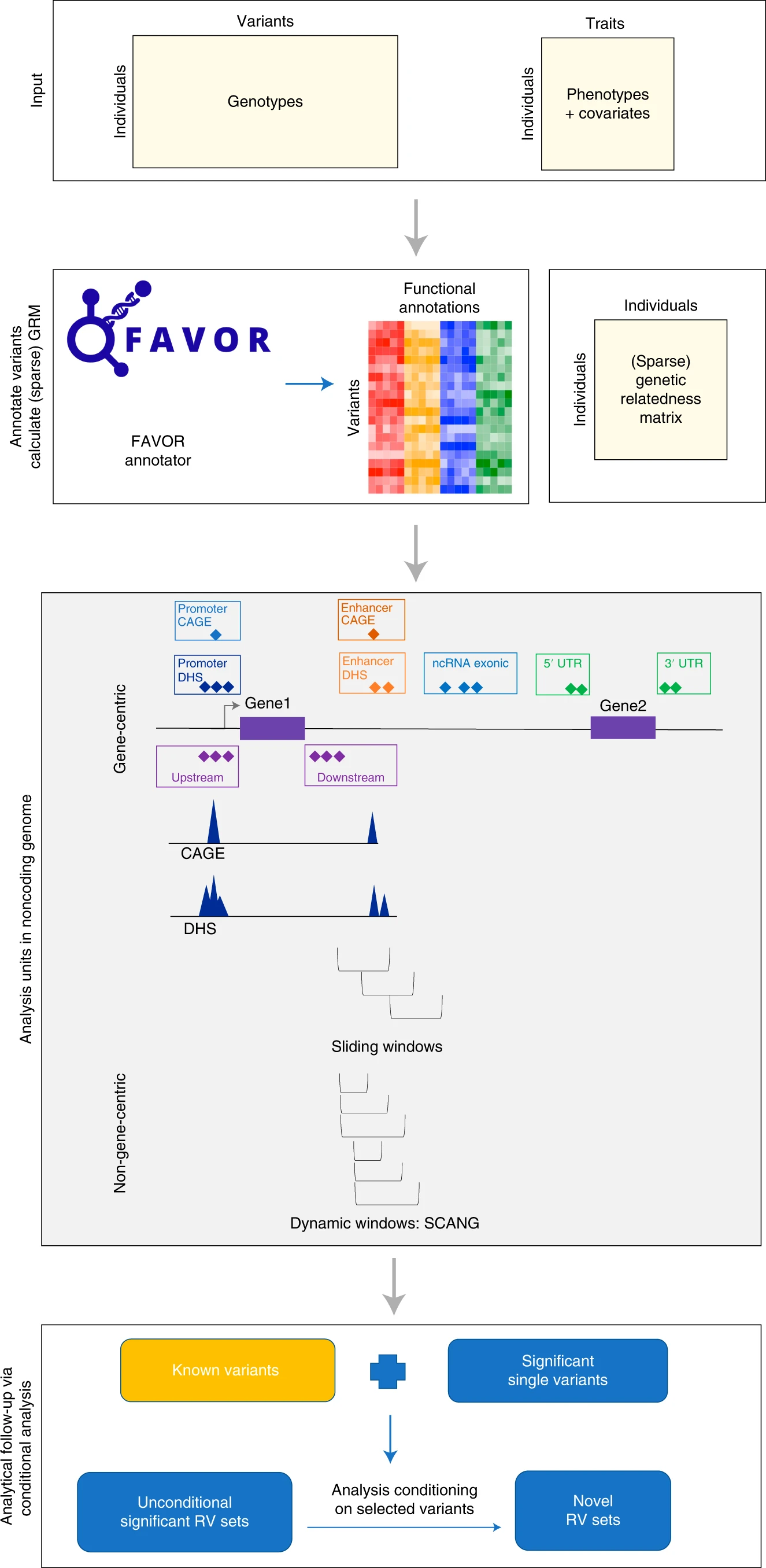
Figure 3: From Li et al NatMeth 2022: a, Prepare the input data of STAARpipeline, including genotypes, phenotypes and covariates. b, Annotate all variants in the genome using FAVORannotator through FAVOR database and calculate the (sparse) GRM. c, Define analysis units in the noncoding genome: eight functional categories of regulatory regions, sliding windows and dynamic windows using SCANG. d, Obtain genome-wide significant associations and perform analytical follow-up via conditional analysis.

Logo image

Maintained by Dylan Lawless. Scientist at EPFL. Resume and Google scholar. RSS feed